Este año he preparado una postal animada con GeoGebra para desearos a todos que paséis unas fiestas estupendas...
Espero que os guste (dadle al botón de START para que comience la animación).
martes, 17 de diciembre de 2013
martes, 10 de diciembre de 2013
CURVAS CÍCLICAS O DE RODADURA
Curvas cíclicas por Jose Antonio Cuadrado
-Link to the wikipedia (English).
-Cycloid
-Epicycloid
-Hypocycloid
Las curvas cíclicas o de rodadura representan la trayectoria de un punto de una circunferencia (llamada RULETA), que rueda sin resbalar, sobre una recta u otra circunferencia (BASE O DIRECTRIZ).
Suelen utilizarse en mecánica (engranajes) y poseen interesantes propiedades que os gustará conocer (al menos eso creo).
Aquí tenéis una estupenda presentación en la que podéis ver las características de cada una de dichas curvas, así como su construcción.
CICLOIDE
Es una curva plana, lugar geométrico de las distintas posiciones de un punto móvil contenido en una circunferencia.
La CICLOIDE puede ser normal si el punto que se desplaza es uno de los de la circunferencia, acortada si es un punto interior y alargada si es exterior.
Trazaremos la recta base o directriz tangente a la circunferencia ruleta o generatiz.
Ese punto de tangencia determina la posición inicial del punto móvil.
La directriz debe tener la medida de la rectificación de la circunferencia.
Por si no recordáis como hacerlo os dejo dos enlaces a una construcción de Mongge:
-Rectificación de la semicircunferencia. (No olvidéis multiplicar la medida resultante por dos).
Debemos dividir después la circunferencia y el segmento en el mismo número de partes iguales. (Es importante saber que el número de partes va a determinar la precisión con la que tracemos la curva).
Ocho partes puede ser un número adecuado. En el caso de la circunferencia realizaría la construcción para inscribir en ella un octógono cuyos vértices determinarían las distintas posiciones del punto en su desplazamiento, es decir al rodar.
Aquí tenéis la construcción en formato MONGGE.
La CICLOIDE tiene una serie de propiedades realmente curiosas:
Es BRAQUISTÓCRONA y TAUTÓCRONA...¿?
Si queréis saber lo que significa esto, no dejéis de ver este sorprendente vídeo.
Accede a la página del profesor de matemáticas autor de este vídeo para saber más sobre la CICLOIDE.
Si quieres practicar enlazada a la imagen tienes una estupenda herramienta de EDUCACIÓNPLASTICA.NET que te ayudará a comprender mejor el trazado de esta curiosa curva cíclica.
Puedes igualmente trazar sus versiones acortada y alargada.
Luis Pérez en su web uno.618, tiene una construcciones interactivas realmente interesantes realizadas con GeoGebra.
En este enlace tenéis las de la cicloide, pero podéis acceder desde ahí a las demás curvas.
EPICICLOIDE
Curva plana (abierta o cerrada), generada por un punto interior, exterior o perteneciente a una circunferencia denominada ruleta, que rueda exteriormente y sin deslizamiento sobre otra circunferencia de tamaño variable llamada directriz. Lógicamente ambas circunferencias pueden tener diferentes relaciones entre sus radio, y en función de ésto la curva que obtendremos tendrá una forma u otra.
Para calcular la longitud del arco que recorrerá la circunferencia ruleta sobre la directriz tras una vuelta completa de la primera, existe una fórmula, que relaciona los radios de ambas: a=360º r/r´. Siendo a el ángulo central de la circunferencia directriz que determina el arco de circunferencia recorrido por la ruleta tras una vuelta.
Así, si r´=2r , el valor del ángulo central recorrido por la ruleta será de 180º.
Pulsa sobre la imagen para acceder sobre la construcción paso a paso de la Epicicloide.
En la imagen tenéis el enlace a la aplicación de educacionplastica.net con la que podréis trazar epicicloides con distintos valores radiales, para comprobar que la curva resultante varía de forma.
Si la circunferencia DIRECTRIZ tiene el mismo tamaño que la RULETA , obtenemos una curva que denominamos CARDIODE (su forma es similar a un corazón). Si la DIRECTRIZ mide el doble que la RULETA , la figura que obtenemos se llama NEFROIDE (se parece a un riñón).
HIPOCICLOIDE
En esta curva ruleta y directriz son, como en la EPICICLOIDE dos circunferencias. La diferencia entre ambas radica en que en éste caso la ruleta rueda dentro de circunferencia directriz.
 Dependiendo de la relación entre los RADIOS de ambas, obtenemos algunas CICLOIDES SINGULARES como puede ser el caso de la HIPOCICLOIDE RECTILÍNEA (transformación del movimiento circular en rectilíneo como ocurre en el caso de la biela-manivela)
Dependiendo de la relación entre los RADIOS de ambas, obtenemos algunas CICLOIDES SINGULARES como puede ser el caso de la HIPOCICLOIDE RECTILÍNEA (transformación del movimiento circular en rectilíneo como ocurre en el caso de la biela-manivela)Imagen: Wikipedia (sitúate sobre ella para ver la animación)

Hipocicloide tricuspidal (ejercicio lámina)
Aquí tenéis el enlace al ejercicio en formato MONGGE
Prueba a cambiar el radio de la circunferencia ruleta y comprueba lo que ocurre. Haz clic aquí
EVOLVENTE DE LA CIRCUNFERENCIA
Es la curva que genera un punto fijo de una recta tangente a una circunferencia que se desplaza alrededor de ella sin resbalar.
Os dejo enlazada la lámina que vamos a realizar, por si queréis repetirla.
domingo, 1 de diciembre de 2013
CURVAS TÉCNICAS
Las curvas técnicas (óvalos, ovoides y espirales) están formadas por arcos de circunferencia tangentes entre sí.
Los óvalos y ovoides son curvas planas y cerradas, ya que empiezan y terminan en el mismo punto, compuestas por cuatro arcos de circunferencia tangentes interiores dos a dos.
Los óvalos tienen dos ejes de simetría, mientras que el ovoide (llamado así por su forma de huevo) tan solo dispone uno. Es particularmente interesante que aprendáis a construir el óvalo que sustituye a la elipse en la perspectiva isométrica, y que sería la representación en ese sistema de representación de la circunferencia.
Las espirales son curvas abiertas y planas generadas por un punto que se aleja del núcleo, aumentando constantemente su radio de giro.
Construcción del óvalo conocido el EJE MAYOR
Aquí tenéis en formato Mongge la llave fija que os he encargado hacer y en la que se utiliza esta curva técnica.
OVOIDES
-
Aquí os dejo los ejercicios que vamos a realizar sobre óvalos y ovoides.
ESPIRALES
-ESPIRAL DE CUATRO CENTROS
Otro tipo de espiral que ya vimos al hablar del número de oro, es la conocida como espiral áurea o de Durero y que se obtiene al subdividir un rectángulo áureo en nuevos rectángulos de forma que conserven dichas proporciones.
Aquí podéis ver como trazar el ÓVALO ISOMÉTRICO en las tres caras de un cubo o, lo que es lo mismo, en los tres planos de una isometría.
Aquí tenéis los ejercicios que debéis hacer por si queréis repetirlos o perdéis la fotocopia.
REPRESENTACIÓN DEL CONO Y EL CILINDRO EN PERSPECTIVA ISOMÉTRICA.
- Representación del cono (Mongge)
- Representación del cilindro (Mongge)
Imprime los siguientes ejercicios sobre el cono y el cilindro. Es importante que te fijes en colocación de la escuadra y el cartabón (o del cartabón y la regla) para trazar los ejes X, Y y Z en perspectiva isométrica.
Os dejo estos dibujos, para que os ayuden a trazar las siguientes figuras de revolución (Cono, cilindro y cono truncado) y así pongáis en práctica el trazado que habéis aprendido a realizar para representar mediante un ÓVALO la PERSPECTIVA ISOMÉTRICA de una CIRCUNFERENCIA sobre cualquiera de los tres PLANOS.
Los óvalos y ovoides son curvas planas y cerradas, ya que empiezan y terminan en el mismo punto, compuestas por cuatro arcos de circunferencia tangentes interiores dos a dos.
Los óvalos tienen dos ejes de simetría, mientras que el ovoide (llamado así por su forma de huevo) tan solo dispone uno. Es particularmente interesante que aprendáis a construir el óvalo que sustituye a la elipse en la perspectiva isométrica, y que sería la representación en ese sistema de representación de la circunferencia.
Las espirales son curvas abiertas y planas generadas por un punto que se aleja del núcleo, aumentando constantemente su radio de giro.
ÓVALOS
Construcción del óvalo conocido el EJE MAYOR
Aquí tenéis en formato Mongge la llave fija que os he encargado hacer y en la que se utiliza esta curva técnica.
OVOIDES
Os dejo la construcción del OVOIDE conocido su eje mayor CD mediante una animación de Mongge.
-
Aquí os dejo los ejercicios que vamos a realizar sobre óvalos y ovoides.
ESPIRALES
-ESPIRAL DE CUATRO CENTROS
Otro tipo de espiral que ya vimos al hablar del número de oro, es la conocida como espiral áurea o de Durero y que se obtiene al subdividir un rectángulo áureo en nuevos rectángulos de forma que conserven dichas proporciones.
Aquí podéis ver como trazar el ÓVALO ISOMÉTRICO en las tres caras de un cubo o, lo que es lo mismo, en los tres planos de una isometría.
Aquí tenéis los ejercicios que debéis hacer por si queréis repetirlos o perdéis la fotocopia.
REPRESENTACIÓN DEL CONO Y EL CILINDRO EN PERSPECTIVA ISOMÉTRICA.
- Representación del cilindro (Mongge)
Imprime los siguientes ejercicios sobre el cono y el cilindro. Es importante que te fijes en colocación de la escuadra y el cartabón (o del cartabón y la regla) para trazar los ejes X, Y y Z en perspectiva isométrica.
Os dejo estos dibujos, para que os ayuden a trazar las siguientes figuras de revolución (Cono, cilindro y cono truncado) y así pongáis en práctica el trazado que habéis aprendido a realizar para representar mediante un ÓVALO la PERSPECTIVA ISOMÉTRICA de una CIRCUNFERENCIA sobre cualquiera de los tres PLANOS.
Podéis modificar en este applet de GeoGebra tanto el radio de la base como la altura total del cono sin seccionar y la distancia respecto de la base a la que se da el corte.
En este caso el plano es paralelo a la base y por eso obtenemos una nueva circunferencia, que al ser representada en perspectiva aparece como un óvalo isométrico.
Aunque lo habitual es que esas CIRCUNFERENCIAS en perspectiva formen parte de piezas más complejas.
jueves, 21 de noviembre de 2013
EJERCICIOS DE TANGENCIAS
-Piezas con tangencias
Aquí tenéis un pequeño vídeo explicándoos una de las piezas que os dí. Contiene tangencias básicas entre rectas y circunferencias (tangente común exterior a dos circunferencias dadas) y entre circunferencias ( con un arco de circunferencia de radio conocido). Tan sólo tenéis que recordar las CONDICIONES DE TANGENCIA en ambos casos:
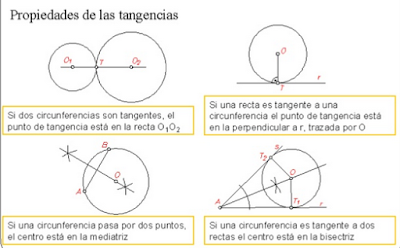
- En el caso de la tangencia entre rectas y circunferencias, debéis recordar que el radio que pasa por el punto de tangencia siempre es perpendicular a la recta.
- Si hablamos de tangencias entre circunferencias deberéis saber que el punto de tangencia entre ambas está en la linea que une sus centros.
 Aquí os dejo resueltas en formato Mongge siete de las piezas que os encargué hacer (la octava la tenéis en el vídeo):
Aquí os dejo resueltas en formato Mongge siete de las piezas que os encargué hacer (la octava la tenéis en el vídeo):
-Pieza 1
-Pieza 2
-Pieza 3
-Pieza 4
-Pieza 5
-Pieza 7
-Pieza 8
Si os situáis sobre la imagen veréis en funcionamiento el mecanismo piñón-cremallera (en este caso con un tornillo sin fin), que transforma el movimiento lineal en circular y que se vale, como otros muchos, del uso de tangencias (circunferencia tangente a una recta en este caso).
Podéis encontrar tangencias igualmente en los sistemas de engranajes con cadena (tangentes comunes exteriores a dos circunferencias), y en los sistemas de poleas con correa.
Os dejo este vídeo que hice con un programa de simulación llamado Algodoo para Tecnologías de 1º de ESO, en el que reconoceréis, supongo, una pieza denominada "engranaje loco" que, al colocarse entre otros dos engranajes, se encarga de que ambos giren en el mismo sentido, sin modificar por ello su relación de transmisión.
Aquí tenéis un montón de láminas para que realicéis piezas industriales con tangencias (algunas de ellas ya las habéis hecho).
En muchas ocasiones deberemos aplicar una escala a la hora de representar piezas industriales u otros objetos cuyo tamaño puede ser mayor o menor que el del soporte.
Tenéis una buena explicación sobre como realizar escalas gráficas en la página Dibujotécnico.com.
Aquí tenéis un pequeño vídeo explicándoos una de las piezas que os dí. Contiene tangencias básicas entre rectas y circunferencias (tangente común exterior a dos circunferencias dadas) y entre circunferencias ( con un arco de circunferencia de radio conocido). Tan sólo tenéis que recordar las CONDICIONES DE TANGENCIA en ambos casos:
- En el caso de la tangencia entre rectas y circunferencias, debéis recordar que el radio que pasa por el punto de tangencia siempre es perpendicular a la recta.
- Si hablamos de tangencias entre circunferencias deberéis saber que el punto de tangencia entre ambas está en la linea que une sus centros.
 Aquí os dejo resueltas en formato Mongge siete de las piezas que os encargué hacer (la octava la tenéis en el vídeo):
Aquí os dejo resueltas en formato Mongge siete de las piezas que os encargué hacer (la octava la tenéis en el vídeo):-Pieza 1
-Pieza 2
-Pieza 3
-Pieza 4
-Pieza 5
-Pieza 7
-Pieza 8
Si os situáis sobre la imagen veréis en funcionamiento el mecanismo piñón-cremallera (en este caso con un tornillo sin fin), que transforma el movimiento lineal en circular y que se vale, como otros muchos, del uso de tangencias (circunferencia tangente a una recta en este caso).
Podéis encontrar tangencias igualmente en los sistemas de engranajes con cadena (tangentes comunes exteriores a dos circunferencias), y en los sistemas de poleas con correa.
Os dejo este vídeo que hice con un programa de simulación llamado Algodoo para Tecnologías de 1º de ESO, en el que reconoceréis, supongo, una pieza denominada "engranaje loco" que, al colocarse entre otros dos engranajes, se encarga de que ambos giren en el mismo sentido, sin modificar por ello su relación de transmisión.
Aquí tenéis un montón de láminas para que realicéis piezas industriales con tangencias (algunas de ellas ya las habéis hecho).
En muchas ocasiones deberemos aplicar una escala a la hora de representar piezas industriales u otros objetos cuyo tamaño puede ser mayor o menor que el del soporte.
Tenéis una buena explicación sobre como realizar escalas gráficas en la página Dibujotécnico.com.
jueves, 14 de noviembre de 2013
TANGENCIAS Y ENLACES
El próximo tema que vamos a estudiar es el de TANGENCIAS Y ENLACES centrándonos en los casos más básicos.
Una vez que sepamos hacerlas, realizaremos una serie de piezas que las contienen.
Os dejo una presentación en la que vais a encontrar los casos más relevantes explicados paso a paso.
Ana Isabel Sánchez tiene una serie de vÍdeos sobre tangencias realmente interesantes. Si quieres verlos PULSA AQUÍ
TANGENCIAS ENTRE RECTAS Y CIRCUNFERENCIAS
Rectas tangentes a una circunferencia que pasen por un punto exterior P: Resolución paso a paso.
Para resolver este ejercicio vamos a reducirlo a uno más sencillo que es el que hemos visto antes, es decir, hallar las rectas tangentes a una circunferencia pasando por un punto exterior P. Para ello, restamos el radio de la circunferencia de menor tamaño a la de mayor radio (ojo hay que restarlo desde un punto de la circunferencia mayor). Si trazamos las rectas tangentes a la circunferencia resultante desde O2 obtendremos dos rectas paralelas a las soluciones que buscamos.
Rectas tangentes comunes interiores a dos circunferencias.
En este caso deberemos sumar a la circunferencia mayor el radio de la menor, para obtener las tangentes solución como paralelas a las trazadas a la circunferencia de radio la suma de los de las dos circunferencias desde el centro-punto O2 (volvemos a simplificar el ejercicio para trabajar con el primero de los supuestos).
Os dejo estos tres ejercicios también en formato Mongge.
A veces se nos puede dar el caso de que necesitemos trazar la recta tangente a un arco de centro inaccesible. Puede resolverse de la siguiente forma.
Aquí tenéis resueltos en formato MONGGE los casos más importantes de TANGENCIAS Y ENLACES BÁSICOS.
-Tangencias básicas entre rectas y circunferencias (conocido el radio de la circunferencia)
-Tangencias básicas entre rectas y circunferencias (desconociendo el radio)
Dos de estos tres ejercicios os los dejo también en formato GeoGebra. El tercero lo hicimos también cuando vimos el incentro de un triángulo y los exincentros de las circunferencias exinscritas.
-
Y en el vídeo tenéis resuelto otro de los ejercicios que vamos a realizar.
TANGENCIAS ENTRE CIRCUNFERENCIAS
El punto de tangencia entre dos circunferencias está en la línea que une sus centros.
-Tangencias entre circunferencias
-Circunferencias tangentes a otras dos (es el ejercicio que tenéis debajo en la construcción de GeoGebra).
-Circunferencias tangentes a otras dos II
ENLACES
-Enlaces
-Enlaces sobre una línea poligonal quebrada
TANGENCIAS SECUNDARIAS
Aquí tenéis los enlaces para acceder a los ejercicios en formato Mongge:- Circunferencias del mismo radio tangentes entre sí y a los lados de un triángulo equilátero.
- n circunferencias tangentes entre sí y a su vez tangentes a otra (en este caso 8).
TANGENCIAS POR HOMOTECIA
Tenéis los ejercicios enlazados a las dos imágenes.
Aquí tenéis resuelto el primero de los ejercicios en formato Mongge.
Y en este otro enlace tenéis la solución del segundo.
Aparte de los ejercicios que ya os he dado, haremos estos otros en clase (os los dejo enlazados por si los queréis repetir):
-Tangencias básicas (fundamentos).
El curso que viene veréis otro tipo de ejercicios de tangencias algo más complejos. No obstante, en ocasiones aparecen ejercicios bastante sencillos en las pruebas PAU o EvAU. Ejercicios como los cuatro que tenéis en esta playlist.
miércoles, 6 de noviembre de 2013
GIROS:EJERCICIOS DE APLICACIÓN
A pesar de que realizar un giro es relativamente sencillo, es difícil sin embargo "ver" en que ocasiones un ejercicio de transformaciones geométricas debe resolverse mediante un giro.
Os dejo uno de los que vamos a realizar sobre papel, en formato Mongge, para que podáis ver el procedimiento por pasos. Se trata del ejercicio nª 11.
Como podréis ver se puede resolver de dos formas:
En la primera de ellas giraremos la circunferencia 60º, y en la segunda, que os dejo enlazada giraremos la recta el mismo ángulo. El centro de giro será el punto A, que es a su vez uno de los vértices del triángulo equilátero que me piden (hay dos posibles soluciones).
Aquí tenéis el enlace al segundo método para resolver el ejercicio.
Os dejo igualmente un Applet de GeoGebra con este ejercicio para que podáis "manipular" la construcción y modificar los datos iniciales. Aquí tenéis resuelto otro ejercicio de giros que presenta también cierta dificultad.
Se trata en este caso de dibujar los posibles cuadrados que tienen dos de sus vértices apoyados sobre las rectas dadas, conociendo además uno de ellos.
Existen múltiples variantes de este ejercicio, ya que se os pueden dar dos rectas paralelas, o bien pediros un triángulo equilátero en vez de un cuadrado.
Tened en cuenta que si las rectas son paralelas las dos soluciones posibles tendrán el mismo tamaño, y que si las rectas son convergentes el tamaño será diferente, tanto en el caso del cuadrado como del triángulo.
 Para que podáis comprender mejor como funcionan este tipo de ejercicios os he preparado un Applet de GeoGebra, para que podáis modificar los parámetros y comprobar como en todos los casos podemos conseguir dos triángulos equiláteros apoyados sobre ambas rectas tras girar una de ellas 60º tomando como centro de giro el vértice A, hasta que ésta se corte con la otra en otro de los vértices, con lo que contaré ya con el lado del triángulo equilátero.
Para que podáis comprender mejor como funcionan este tipo de ejercicios os he preparado un Applet de GeoGebra, para que podáis modificar los parámetros y comprobar como en todos los casos podemos conseguir dos triángulos equiláteros apoyados sobre ambas rectas tras girar una de ellas 60º tomando como centro de giro el vértice A, hasta que ésta se corte con la otra en otro de los vértices, con lo que contaré ya con el lado del triángulo equilátero.
Probad a situar el punto A en otro lugar o cambiad la inclinación de las rectas, para comprobar que el resultado se mantiene (varía el tamaño de los triángulos, pero siguen siendo equiláteros).
Es interesante también que comprobéis que el resultado es el mismo tanto si giramos la recta r como si lo hacemos con s. (Tenéis el ejercicio enlazado a la imagen)
Debajo tenéis otra construcción pero en este caso lo que se nos pide trazar no es un triángulo, sino un cuadrado con un vértice apoyado sobre cada recta y el tercero en A, con lo que el giro deberá hacerse de 90º que es el ángulo que existe entre dos vértices consecutivos del polígono (en el caso del triángulo, éste era de 60º).
Aquí tenéis otro ejercicio de aplicación del mismo concepto.
Os dejo uno de los que vamos a realizar sobre papel, en formato Mongge, para que podáis ver el procedimiento por pasos. Se trata del ejercicio nª 11.
Como podréis ver se puede resolver de dos formas:
En la primera de ellas giraremos la circunferencia 60º, y en la segunda, que os dejo enlazada giraremos la recta el mismo ángulo. El centro de giro será el punto A, que es a su vez uno de los vértices del triángulo equilátero que me piden (hay dos posibles soluciones).
Aquí tenéis el enlace al segundo método para resolver el ejercicio.
Os dejo igualmente un Applet de GeoGebra con este ejercicio para que podáis "manipular" la construcción y modificar los datos iniciales. Aquí tenéis resuelto otro ejercicio de giros que presenta también cierta dificultad.
Se trata en este caso de dibujar los posibles cuadrados que tienen dos de sus vértices apoyados sobre las rectas dadas, conociendo además uno de ellos.
Existen múltiples variantes de este ejercicio, ya que se os pueden dar dos rectas paralelas, o bien pediros un triángulo equilátero en vez de un cuadrado.
Tened en cuenta que si las rectas son paralelas las dos soluciones posibles tendrán el mismo tamaño, y que si las rectas son convergentes el tamaño será diferente, tanto en el caso del cuadrado como del triángulo.
 Para que podáis comprender mejor como funcionan este tipo de ejercicios os he preparado un Applet de GeoGebra, para que podáis modificar los parámetros y comprobar como en todos los casos podemos conseguir dos triángulos equiláteros apoyados sobre ambas rectas tras girar una de ellas 60º tomando como centro de giro el vértice A, hasta que ésta se corte con la otra en otro de los vértices, con lo que contaré ya con el lado del triángulo equilátero.
Para que podáis comprender mejor como funcionan este tipo de ejercicios os he preparado un Applet de GeoGebra, para que podáis modificar los parámetros y comprobar como en todos los casos podemos conseguir dos triángulos equiláteros apoyados sobre ambas rectas tras girar una de ellas 60º tomando como centro de giro el vértice A, hasta que ésta se corte con la otra en otro de los vértices, con lo que contaré ya con el lado del triángulo equilátero.Probad a situar el punto A en otro lugar o cambiad la inclinación de las rectas, para comprobar que el resultado se mantiene (varía el tamaño de los triángulos, pero siguen siendo equiláteros).
Es interesante también que comprobéis que el resultado es el mismo tanto si giramos la recta r como si lo hacemos con s. (Tenéis el ejercicio enlazado a la imagen)
Debajo tenéis otra construcción pero en este caso lo que se nos pide trazar no es un triángulo, sino un cuadrado con un vértice apoyado sobre cada recta y el tercero en A, con lo que el giro deberá hacerse de 90º que es el ángulo que existe entre dos vértices consecutivos del polígono (en el caso del triángulo, éste era de 60º).
Aquí tenéis otro ejercicio de aplicación del mismo concepto.
martes, 29 de octubre de 2013
lunes, 21 de octubre de 2013
EQUIVALENCIAS
Decimos que dos superficies planas son equivalentes cuando tienen distinta forma e igual área.
En el caso de la imagen podemos apreciar que los tres triángulos tienen la misma base y la misma altura.
Dado que el área de un triángulo equivale al producto de la base por la altura, podemos asegurar que en los tres casos la superficie es la misma.

Podemos obtener también un rectángulo equivalente a un triángulo.
Éste tendrá la misma base y la mitad de la altura del triángulo, ya que el área de ambos será base x altura/2
Las figuras están coloreadas así para que podamos apreciar su equicomposición, es decir, las formas de las que están compuestas ambas son las mismas.
Podemos con facilidad eliminar un lado de un polígono ya que los triángulos son equivalentes si manteniendo su base, su altura no se modifica.
De esta forma podemos eliminar uno o más lados de cualquier polígono, hasta convertirlo si así lo deseamos en un triángulo equivalente al polígono de partida.
CUADRADO EQUIVALENTE A UN RECTÁNGULO
CUADRADO EQUIVALENTE A UN CUADRILÁTERO
En cuanto al método para convertir un cuadrilátero cualquiera en un cuadrado equivalente, pasa por descomponer el cuadrilátero en dos triángulos de lado común (una de las diagonales del cuadrilátero). Y una vez hallado el rectángulo equivalente al cuadrilátero, estaremos en el caso anterior.
CUADRADO EQUIVALENTE A UN CÍRCULO
Para realizar este ejercicio debemos saber rectificar la semicircunferencia. De esta forma tendríamos el valor de πr.
Existen varios métodos para realizar la rectificación de una circunferencia. El método que os muestro aquí permite rectificar de una forma muy sencilla la semicircunferencia (ojo con esto, si quisiéramos hallar el valor de la rectificación de la circunferencia deberíamos multiplicar por dos el resultado). La rectificación de una semicircunferencia equivale a la suma de los lados del cuadrado y del triángulo inscritos en ella.
Para hacer los ejercicios en papel imprime esta lámina.
EJERCICIOS MÁS COMPLEJOS:
Aquí tenéis la solución a un ejercicio sobre equivalencias que salió en Selectividad en Murcia en el 2001. Se trata de un ejercicio algo más complejo que los que hemos hecho hasta ahora, pero probablemente tras ver el vídeo no os lo parecerá tanto.
Otro posible ejercicio es el que os propongo a continuación. Se trata de trazar el triángulo equilátero equivalente a un cuadrado determinado.Y aquí os dejo otro ejercicio parecido que apareció en la PAU de Murcia en el 2003.
domingo, 22 de septiembre de 2013
OPERACIONES CON SEGMENTOS
Os lo dejo enlazado, porque en esta ocasión es de un tamaño mucho mayor. Tan solo tenéis que hacer clic sobre la imagen para acceder a la construcción.
Imprime la lámina que vamos a realizar.
-Producto de segmentos
-División de segmentos
-Tercera proporcional:
Es la igualdad de dos razones (fracciones) en las que conocidos dos elementos, uno de los cuales se repite (en dichas fracciones sus extremos o sus medios se repiten).
En la fracción"x" es la tercera proporcional entre a y b (a/b y b/x serían fracciones equivalentes)
Imprime la lámina que vamos a realizar.
-Producto de segmentos
-División de segmentos
-Tercera proporcional:
Es la igualdad de dos razones (fracciones) en las que conocidos dos elementos, uno de los cuales se repite (en dichas fracciones sus extremos o sus medios se repiten).
En la fracción"x" es la tercera proporcional entre a y b (a/b y b/x serían fracciones equivalentes)
- Cuarta proporcional:
Es la igualdad de dos razones (fracciones), en la que son conocidos tres de sus elementos y desconocido el cuarto. La forma típica de una cuarta proporcional es a/b = c/x, donde a, b y c, son los tres segmentos conocidos, y x la incógnita.
Si a=4 cm y b=2 cm, y conocemos el lado mayor de un segundo rectángulo semejante , c=6 cm, podríamos determinar gráficamente el valor de su otro lado (x=3)
miércoles, 5 de junio de 2013
ABATIMIENTO DE UNA FIGURA PLANA (II)
Aquí tenéis un ejercicio muy similar a éste. En este caso la figura plana es un pentágono regular. Por si no recordáis como se hace el pentágono inscrito en una circunferencia aquí lo tenéis.
Intenta realizar en papel estos dos ejercicios, así como esta otra lámina
Debajo tenéis los ejercicios 17.1, 17.2 y 18.3 resueltos.
Intenta realizar en papel estos dos ejercicios, así como esta otra lámina
Debajo tenéis los ejercicios 17.1, 17.2 y 18.3 resueltos.
martes, 28 de mayo de 2013
PLANO PERPENDICULAR A OTROS DOS
Para que un plano sea perpendicular a otros dos, deberá ser perpendicular a la recta intersección de los dos primeros (recordad que si una recta y un plano son perpendiculares, esa perpendicularidad se reflejará en sus proyecciones).
Os dejo un vídeo de aitoreche, en el que resuelven este mismo ejercicio de otra forma.
En este caso, en vez de hallar la recta intersección de ambos planos, se hacen pasar por el punto, dos rectas perpendiculares cada una de ellas a uno de los dos planos dados, y finalmente se determina el plano uniendo las trazas homónimas de ambas rectas.
AQUÍ lo tenéis resuelto en Mongge con los mismos datos que en el caso anterior, de forma que comprobéis que el resultado en ambos casos es el mismo.
Vosotros decidís de que forma os resulta más cómodo realizar el ejercicio o como lo entendéis mejor.
PERPENDICULARIDAD ENTRE PLANOS
Dos planos serán perpendiculares entre sí, si uno de ellos contiene una recta perpendicular al otro plano.
Si lo que queremos es trazar un plano perpendicular a otro conteniendo un punto, deberemos hacer pasar por dicho punto una recta perpendicular a dicho plano para determinar las trazas del plano buscado.
Si además me piden que uno de los planos contenga a una recta, deberemos recordar que dos rectas que se cortan definen un plano. Si además una de ellas es perpendicular al otro plano, el plano que determinen también lo será.
AQUÍ está el ejercicio resuelto (13.1)
Otro de los ejercicios que vamos a ver consiste en el trazado del plano que pasa por la Línea de Tierra y que es perpendicular a otro paralelo a ella.(13.3)
viernes, 24 de mayo de 2013
DISTANCIA PUNTO-PLANO
La determinación de distancias es la aplicación más usual de la perpendicularidad.
Os enlazo otro ejercicio similar a éste. En este caso el plano es paralelo a la Línea de Tierra con lo cual la distancia entre el punto y el plano se verá en Verdadera Magnitud en el plano de perfil. AQUÍ tenéis el ejercicio resuelto.
EJERCICIO 12.2
En el siguiente ejercicio hallaremos dicha distancia tan sólo en proyecciones, aunque lo realmente interesante será hallar la verdadera magnitud de dicha distancia (ese será el siguiente concepto que aprenderemos).
Tenéis el ejercicio en dos formatos. En el caso del vídeo está explicado paso a paso, pero os lo subo también en formato MONGGE para que podáis verlo al ritmo que queráis.
Os enlazo otro ejercicio similar a éste. En este caso el plano es paralelo a la Línea de Tierra con lo cual la distancia entre el punto y el plano se verá en Verdadera Magnitud en el plano de perfil. AQUÍ tenéis el ejercicio resuelto.
EJERCICIO 12.2
sábado, 11 de mayo de 2013
SECCIÓN: PIRÁMIDE RECTA POR PLANO OBLICUO
Este ejercicio podríais resolverlo ya, realizando la intersección de un plano oblicuo con las aristas de la pirámide que son a su vez rectas oblicuas (utilizando para ello planos proyectantes).
Por si no recordáis como hacerlo aquí tenéis el método.
El próximo año utilizaréis un método que simplifica la resolución del ejercicio y que consiste en aprovechar la relación de homología que existe entre la base y la sección producida por el plano secante (es el que he usado en este caso).
Comprobad que los lados de la base y de la sección convergen al prolongarlos, en puntos dobles situados sobre la traza horizontal del plano.
Imprime ésta lámina y realiza las intersecciones de pirámide y prisma con sendos planos oblicuos.
Por si no recordáis como hacerlo aquí tenéis el método.
El próximo año utilizaréis un método que simplifica la resolución del ejercicio y que consiste en aprovechar la relación de homología que existe entre la base y la sección producida por el plano secante (es el que he usado en este caso).
Comprobad que los lados de la base y de la sección convergen al prolongarlos, en puntos dobles situados sobre la traza horizontal del plano.
Imprime ésta lámina y realiza las intersecciones de pirámide y prisma con sendos planos oblicuos.
jueves, 2 de mayo de 2013
Suscribirse a:
Entradas (Atom)